NU-NeRF: Neural Reconstruction of Nested Transparent Objects with Uncontrolled Capture Environment

Accepted by ACM Transactions on Graphics(Proc. of SIGGRAPH Asia 2024)

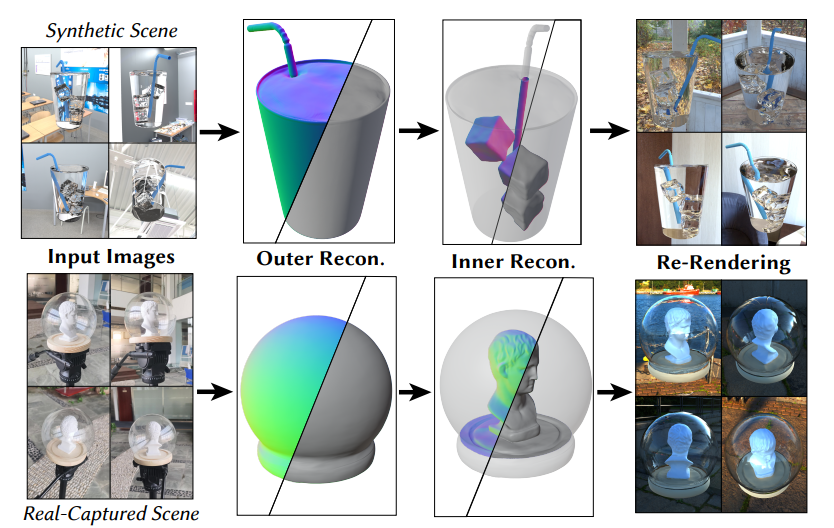
Figure: Given a set of input images of a nested transparent object, our NU-NeRF pipeline can conduct high quality reconstruction of both the outer and inner surfaces in a two-stage manner. The reconstruction results can be used for realistic re-rendering.

The reconstruction of transparent objects is a challenging problem due to the highly noncontinuous and rapidly changing surface color caused by refraction. Existing methods rely on special capture devices, dedicated backgrounds, or ground-truth object masks to provide more priors and reduce the ambiguity of the problem. However, it is hard to apply methods with these special requirements to real-life reconstruction tasks, like scenes captured in the wild using mobile devices. Moreover, these methods can only cope with solid and homogeneous materials, greatly limiting the scope of the application. To solve the problems above, we propose NU-NeRF to reconstruct nested complex transparent objects requiring no dedicated capture environment or additional input. NU-NeRF is built upon a neural signed distance field formulation and leverages neural rendering techniques. It consists of two main stages. In Stage I, the surface color is separated into reflection and refraction. The reflection is decomposed using physically based material and rendering. The refraction is modeled using a single MLP given the refraction and view directions, which is a simple yet effective solution of refraction modeling. This step produces high-fidelity geometry of the outer surface. In stage II, we use explicit ray tracing on the reconstructed outer surface for accurate light transport simulation. The surface reconstruction is executed again inside the outer geometry to obtain any inner surface geometry. In this process, a novel transparent interface formulation is used to cope with different types of transparent surfaces. Experiments conducted on synthetic scenes and real captured scenes show that NU-NeRF is capable of producing better reconstruction results than previous methods and achieves accurate nested surface reconstruction while requiring no dedicated capture environment.

NU-NeRF: Neural Reconstruction of Nested Transparent Objects with Uncontrolled Capture Environment

[Paper and Code]

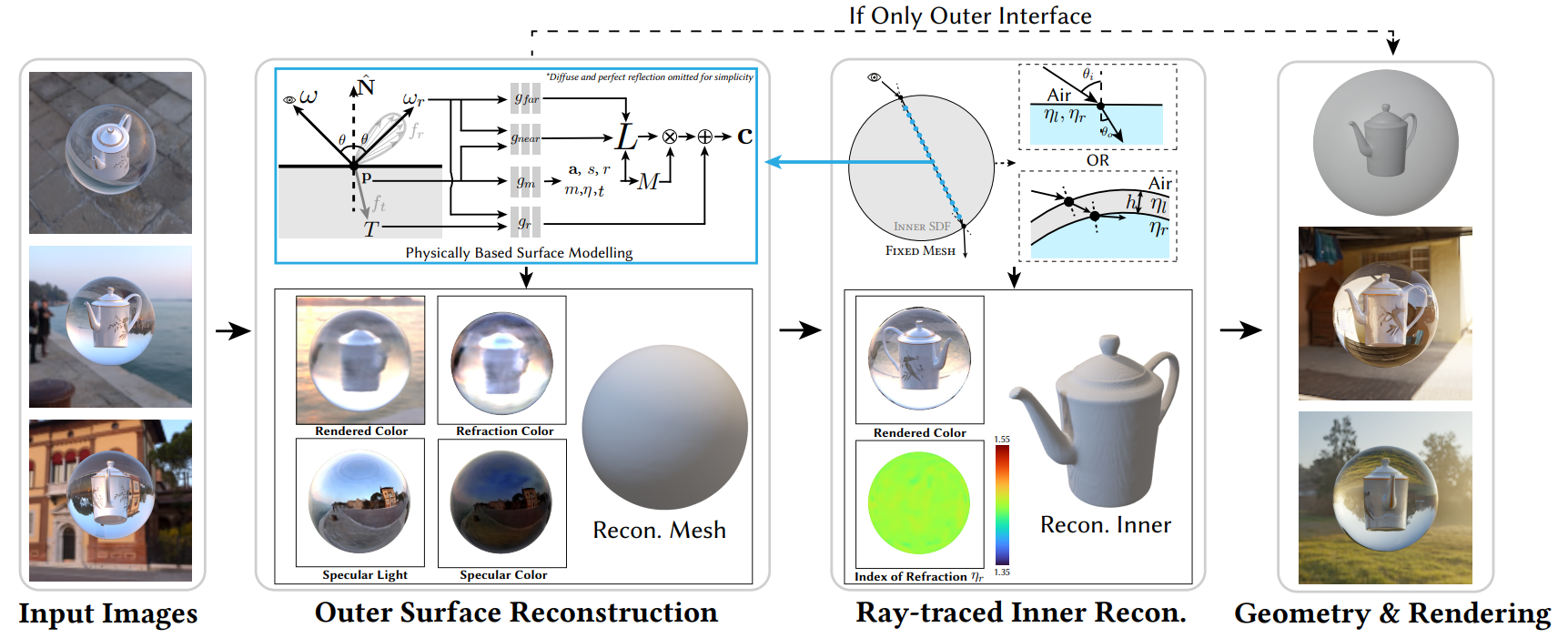
Overview of NU-NeRF

Figure: The overview of NU-NeRF pipeline. Given a set of images of a nested transparent object, the reconstruction pipeline of NU-NeRF is separated into two stages. In the first outer interface reconstruction stage, neural rendering techniques are adopted. For each sample point, the split sum approximation is used to calculate the physically based reflection. Additionally, an MLP is used to predict the refracted light. Despite the blurry result predicted by the refraction MLP, it is vital for high-fidelity reconstruction of the outer geometry. In the second ray-traced inner surface reconstruction stage, the outer interface is modeled using two IoRs and an optional thickness. For each refracted ray, another neural rendering process is executed within the surface to obtain the inner geometry. Note that the surface formulation is used again in the second stage (marked by light blue). Finally, the outer and inner geometry can be merged together for downstream applications.

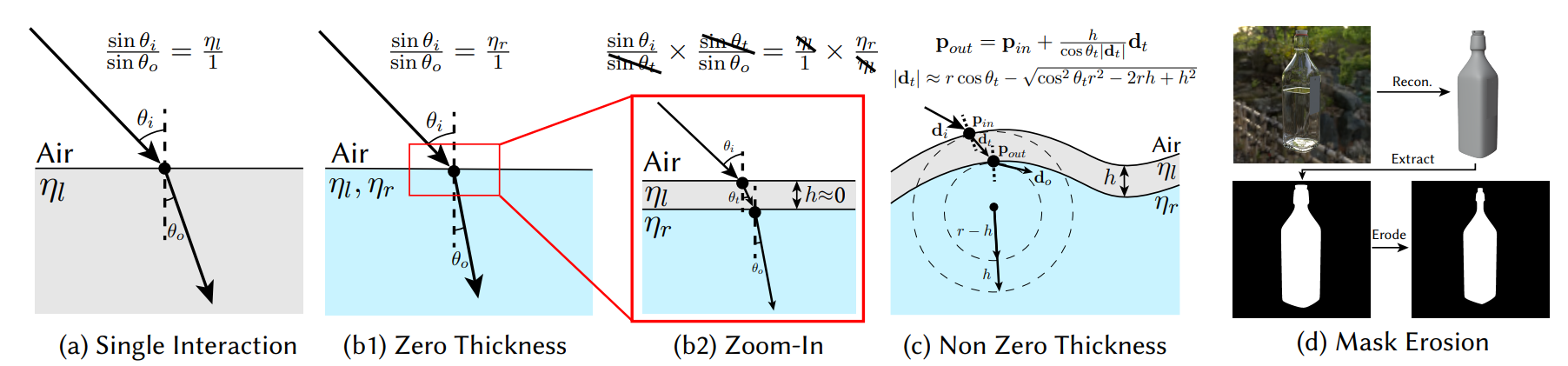
Figure: Zero and non-zero thickness formulations. When reconstructing non-solid objects like containers, two IoRs \eta_l , \eta_l are used to model the interface, corresponding to the IoR of the container itself and the inner substance. For very thin interface which can be regarded as zero-thick, we assume its two faces are parallel, thus the refraction direction only depends on the inner IoR \eta_r . When the thickness can not be ignored, we introduce another parameter h to model the thickness. We additionally use spheres to approximate the local area of the incident position. The normals and outgoing directions at the intersection points can be calculated using analytical calculations. For this type of surface, we utilize an eroded mask to ignore the pixels at the edge of the geometry since the light in that area will undergo complex total internal refraction.

Figure: The definition of surface material. To cope with the transparent refraction, we additionally introduce a "transparent" type of material and use a parameter t to interpolate between "transparent" and the regular "metal and dielectric" material used in previous literature.

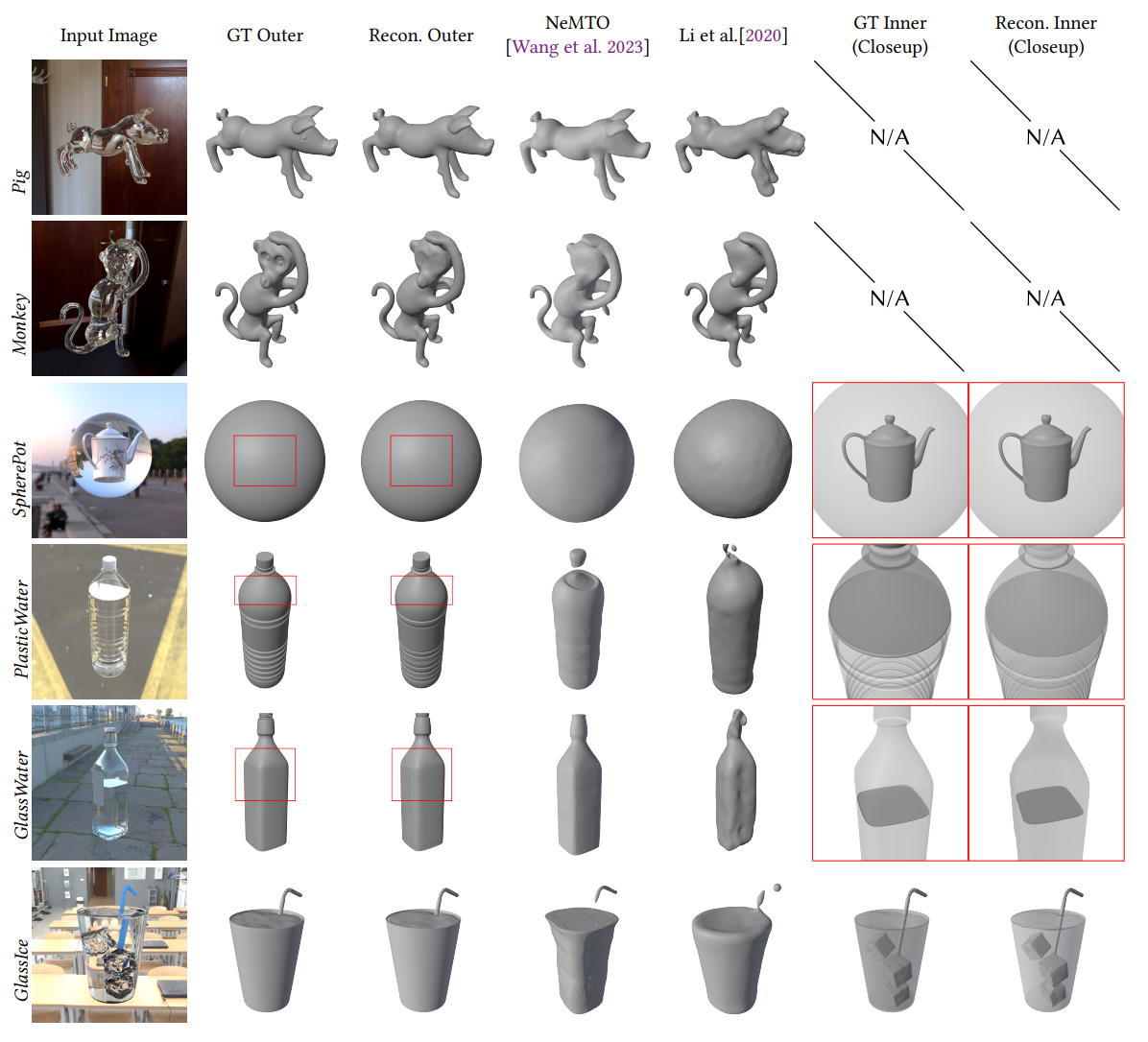
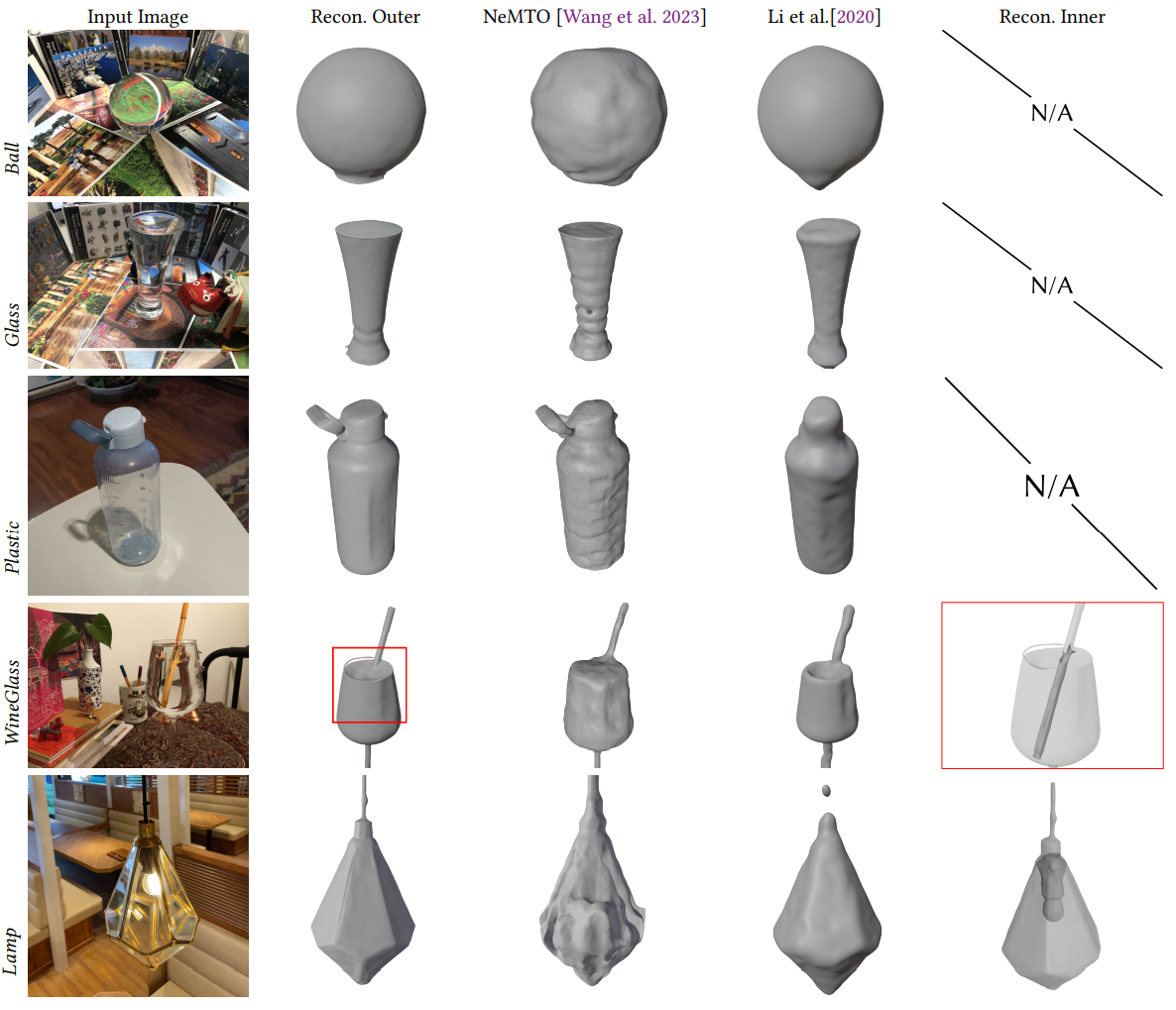
Figure: Reconstruction and Rendering results on synthetic scenes. For each scene, we show the input image, GT inner/outer shapes, reconstructed inner/outer shapes and reconstruction results of NeMTO [Wang et al. 2023] and Li et al. [2020].

Figure: Reconstruction and Rendering results on real scenes. For each scene, we show the input image, reconstructed inner/outer shapes, and reconstruction results of NeMTO [Wang et al. 2023] and Li et al. [2020].

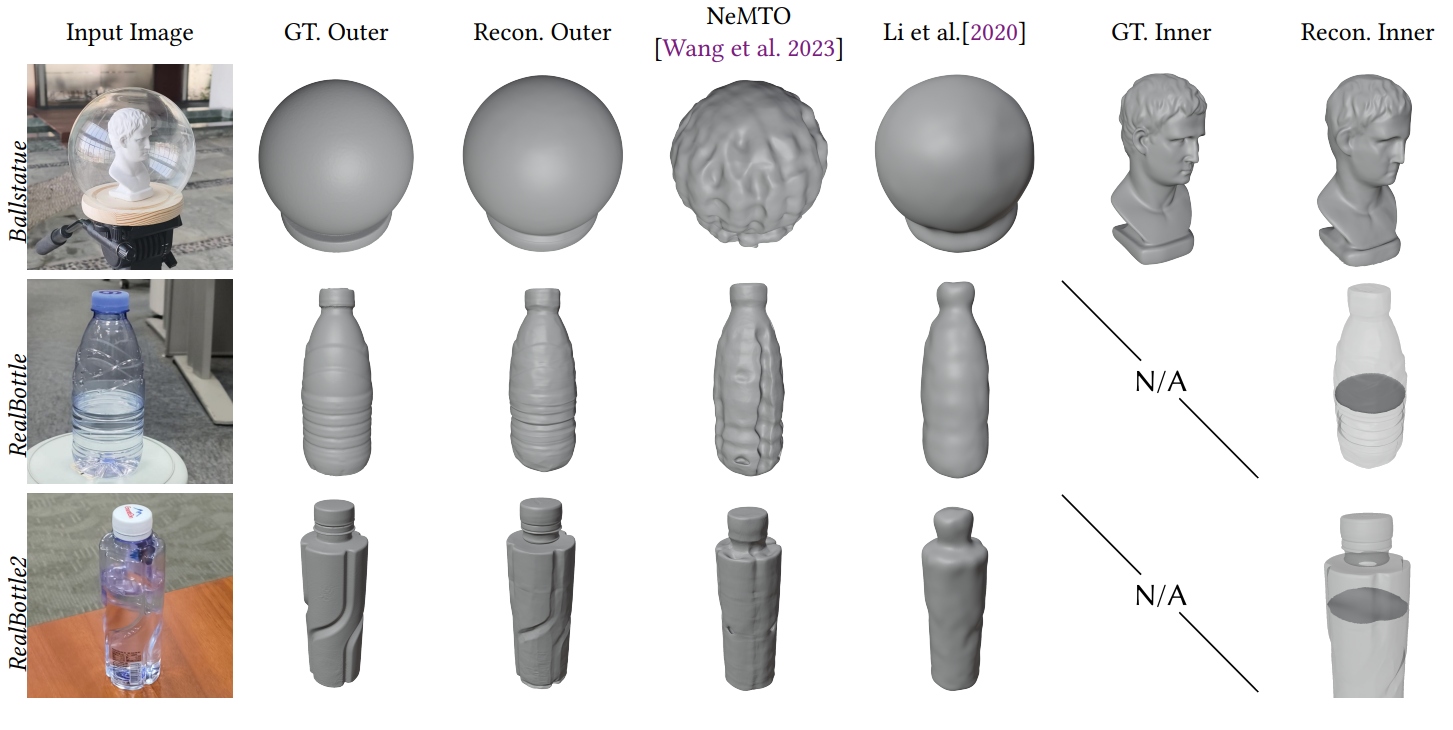
Figure: Reconstruction and Rendering results on real scenes with ground truth geometry captured by ourselves. For each scene, we show the input image, GT inner/outer shapes, reconstructed inner/outer shapes, and reconstruction results of NeMTO [Wang et al. 2023] and Li et al. [2020].