DSG-Net

Figure 1: Our deep generative network DSG-Net encodes 3D shapes with complex structure and fine geometry in a representation that leverages the synergy between geometry and structure, while disentangling these two aspects as much as possible. This enables novel modes of controllable generation for high-quality shapes.Left: results of disentangled interpolation. Here, the top left and bottom right chairs (highlighted with red rectangles) are the input shapes. The remaining chairs are generated automatically with our DSG-Net, where in each row, the structure of the shapes is interpolated while keeping the geometry unchanged, whereas in each column, the geometry is interpolated while retaining the structure. Right: shape generation results with complex structure and fine geometry details by our DSG-Net. We show close-up views in dashed yellow rectangles to highlight local details.

3D shape generation is a fundamental operation in computer graphics. While significant progress has been made, especially with recent deep generative models, it remains a challenge to synthesize high-quality geometric shapes with rich detail and complex structure, in a controllable manner. To tackle this, we introduce DSG-Net, a deep neural network that learns a disentangled structured mesh representation for 3D shapes, where two key aspects of shapes, geometry and structure, are encoded in a synergistic manner to ensure plausibility of the generated shapes, while also being disentangled as much as possible. This supports a range of novel shape generation applications with intuitive control, such as interpolation of structure (geometry) while keeping geometry (structure) unchanged. To achieve this, we simultaneously learn structure and geometry through variational autoencoders (VAEs) in a hierarchical manner for both, with bijective mappings at each level. In this manner we effectively encode geometry and structure in separate latent spaces, while ensuring their compatibility: the structure is used to guide the geometry and vice versa. At the leaf level, the part geometry is represented using a conditional part VAE, to encode high-quality geometric details, guided by the structure context as the condition. Our method not only supports controllable generation applications, but also produces high-quality synthesized shapes, outperforming state-of-the-art methods.

DSG-Net: Disentangled Structured Mesh Netfor Controllable Generation of Fine Geometry

[ArXiv Preprint]

Disentangled but Highly Synergistic Representation of Shape Geometry and Structure Hierarchies

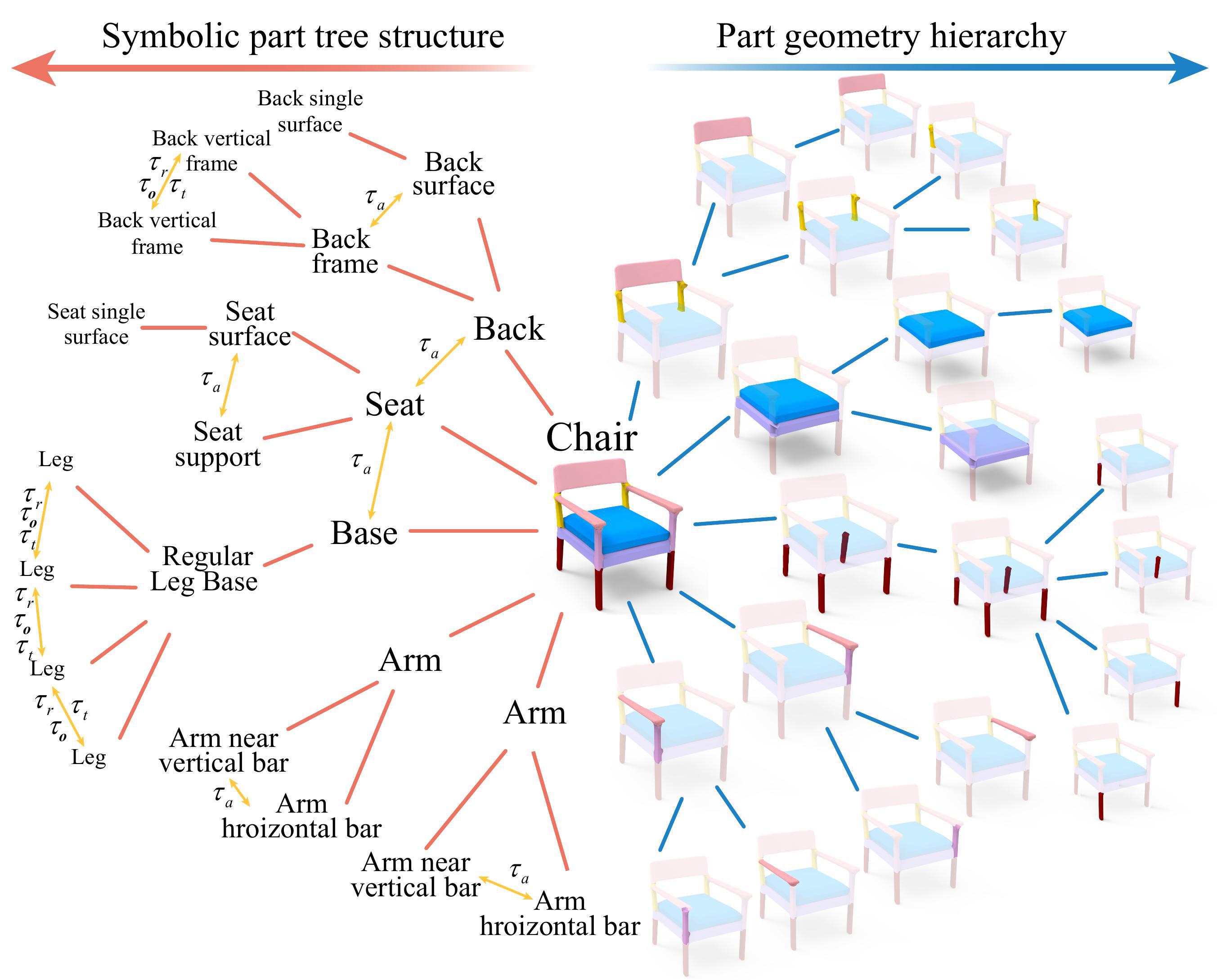
Figure 2: An example showing the proposed disentangled but highly synergistic representation of shape geometry and structure hierarchies. There is a bijective mapping between the tree nodes in the two hierarchies. In the structure hierarchy, we consider symbolic part semantics and a rich set of part relationships (orange arrows), such as adjacency τ_a, translational symmetry τ_t, reflective symmetry τ_r and rotational symmetry τ_o. In the part geometry hierarchy, the part geometry is represented by mesh.

Coupled Hierarchical Graph Network Architecture for Geometry and Structure

Figure 3. Network Architecture: We train two coupled variational autoencoders (VAEs) with recursive encoders and decoders and learn disentangled latent spaces for shape geometry and structure. The left figure illustrates the joint learning procedure of the structure VAE (shown in red) and the geometry VAE (shown in blue). In the encoding stages, the structure features summarize the symbolic part semantics and recursively compute sub-hierarchy structure contexts, while the geometry features encode the detailed part geometry for leaf nodes and propagate the geometry information along the same hierarchy. The decoding procedures of the VAEs are supervised to reconstruct the hierarchical structure and geometry information in an inverse manner. The right figure illustrates the shared message-passing mechanism used in both VAEs among related part nodes in the encoding (top) and decoding (bottom) stages, as well as the matching procedure for simultaneous training of the decoding stages for the two VAEs (middle). The blue and red nodes refer to the part nodes in the geometry and structure hierarchies respectively. For the encoding stage, there are two branches to aggregate the self-information (geometry/structure) of siblings respectively. It performs several message-passing protocols along the relation edge among the siblings and finally gathers into a feature by max-pooling and FC layers for each branch. For the decoding stage, there are also two branches to decode one feature to its siblings for geometry and structure. It predicts existence and the edges among the existed nodes on structure branch. The geometry branch utilizes the predicted relationships. Based on this, the final node features of two branches will be updated by several message-passing protocols.

Figure 4. Shape Generation: Shape generation results. We sample random Gaussian noise vectors and use our DSG-Net to generate realistic shapes with complex structures and detailed geometry. Here we show eight generation results for each of the four object categories in PartNet

Figure 5. Disentangled Generated Shapes: Qualitative results for disentangled shape generation. Given an input shape (a), we extract the geometry code and structure code. We fix one of them, we random sample on the other latent space to generate the new shapes (b). For the first row of (b), we keep the geometry code unchanged and randomly explore the structure latent space. And, for the second row, we keep the structure code unchanged and randomly sample over the geometry latent space.

Figure 6. Shape Interpolation: Shape interpolation results on the four PartNet categories. We linearly interpolate between both the structure and geometry features of the two shapes. In the interpolated steps, we see both continuous geometry variations and discrete structure changes.

Figure 7. Disentangled Shape Interpolation: Qualitative results for disentangled shape interpolation. (a,c,e) and (b,d,f ) respectively show the source and target shapes. The following two rows present the interpolation result in one latent space (geometry or structure) while using the code of the target shape in the other latent space. Concretely, the first row interpolates the structure between two shapes while fixing the geometry code of target shape and the second row interpolates the geometry between two shapes while fixing the structure code of target shape. We see a clear disentanglement of the shape structure and geometry in the interpolated results.

Disentangled but Highly Synergistic Representation of Shape Geometry and Structure Hierarchies

Coupled Hierarchical Graph Network Architecture for Geometry and Structure

Video